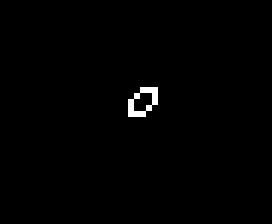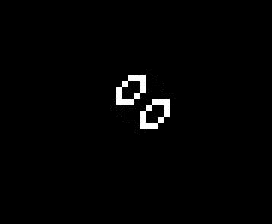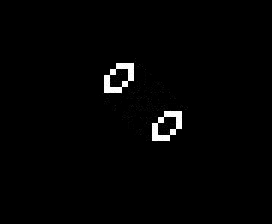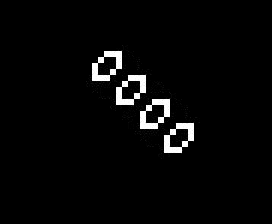In Conway’s Life the rules for the birth and death of cells are simple:
1. Any cell with fewer than two live neighbors dies
2. Any living cell with two or three living neighbors lives
3. Any living cell with more than three living neighbors dies
4. Any dead cell with exactly three living neighbors becomes a living cell
Highlife is a cellular automaton similar to Life except for the addition of a birth rule. Whenever an empty cell is surrounded by 6 live cells a live cell is born so the rules are:
1. Any cell with fewer than two live neighbors dies
2. Any living cell with two or three living neighbors lives
3. Any living cell with more than three living neighbors dies
4. Any dead cell with exactly three living neighbors becomes a living cell
5. Any dead cell with exactly six living neighbors becomes a living cell
Another way to represent this is to use a shorthand notation like the following:
Life B3S23 – Birth 3 neighbors, Survive 2 or 3 neighbors
HighLife B36S23 – Birth 3 or 6 neighbors, Survive 2 or 3 neighbors
The addition of another rule may seem like a small change and many of the same patterns exist in both Life and HighLife but there is an interesting difference. A small simple pattern known as the replicator exists that creates copies of itself every 12 generations. As far as anyone knows a small replicator like this doesn’t exist in Life. So, for that reason, I’ve decided to modify my code so that I can run either Life or HighLife.
Doing so was fairly easy and only involved changing a few lines of code
def updateState(currentState):
'''
This function is where the actual game of life calculations happen
for each cell
'''
nextState = copy.deepcopy(currentState)
#deepcopy could be moved to gol.py. <1% runtime though
neighborCount = scipy.signal.convolve2d(currentState, config.neighbors,
mode="same",boundary="wrap")
#B3/S23
#nextState[np.where((neighborCount != 2) & (neighborCount != 3))] = 0
#nextState[np.where(neighborCount == 3)]= 1
#B36/S23
nextState[np.where((neighborCount != 2) & (neighborCount != 3))] = 0
nextState[np.where(neighborCount == 3)] = 1
nextState[np.where((neighborCount == 6) & (currentState == 0))] = 1
return nextState
I’ve commented out the Life lines of code so that I can switch back and forth easily and added in the HighLife code. When I first did this I made what seemed like a straightforward change of:
def updateState(currentState): nextState[np.where((neighborCount == 3) | (neighborCount == 6))] = 1
however the replicator didn’t work. It took me a while to figure out what was going on and how to correctly implement the rule. What I was missing is that only dead cells with 6 neighbors should become living cells and living cells with 6 neighbors should die. My first attempt didn’t look at the current state but just made the cell live in the next generation. Once I understood this it still took a while to figure out how to correct it. Fortunately the Numpy where function can look at more than one array at a time so the line
def updateState(currentState): nextState[np.where((neighborCount == 6) & (currentState == 0))] = 1
looks at both the number of neighbors and the current state of the cell so that only dead cells become living.
Everything is easy once you know how.
So once I had the new HighLife code working I was able to create the replicator

and let it do its thing. As you can see one replicator first becomes two and then four.